Table of Contents
ABINIT, lesson on the temperature-dependence of the electronic structure (TD)
This lesson aims at showing how to get the following physical properties, for periodic solids :
- The zero-point-motion renormalization (ZPR) of eigenenergies
- The temperature-dependence of eigenenergies
- The lifetime/broadening of eigenenergies
This lesson should take about 1 hour.
Copyright (C) 2005-2014 ABINIT group (XG)
This file is distributed under the terms of the GNU General Public License, see ~abinit/COPYING or http://www.gnu.org/copyleft/gpl.txt.
For the initials of contributors, see ~abinit/doc/developers/contributors.txt.
General note
At the time of writting (June 2014), there are two ways to compute the temperature dependence with Abinit:
- Using Anaddb: historically the first coded way. This option does not require the use of Netcdf
- Using post-processing python scripts: this is the recommended way as it provide more options and is more optimal (take less disk space and is less memory demanding). This option REQUIRED the use of Netcdf (both for Abinit and for python). To install Abinit with Netcdf please see the following link (SP: TO BE ADDED). You should also install netcdf for python. Informations can be found here.
For the theory related to the temperature dependence calculations, you can read the following papers:
This tutorial can only be done with Abinit 7.9.1 and higher.
1. Calculation of the ZPR of eigenenergies at $\mathbf{q}=\mathbf{\Gamma}$
All the inputs files are located in ~/abinit/tests/tutorespfn/Input/temp_x and the reference files in ~/abinit/tests/tutorespfn/Refs/temp_x but we will provide here all the input files that you can copy/paste to any place that suits you to do the calculations.
First, run the calculation using the following temp_1.in input file
- temp_1.in
# C in diamond structure. ndtset 3 elph2_imagden 0.1 eV # Imaginary shift of the denominator of the sum-over-states # in the perturbation denominator. Usual value is 0.1 eV to reproduce # experimental broadening at 300K. Increasing the value help the # convergence with respect to the number of q-points. ngkpt 2 2 2 # k-grid should be at least 4x4x4 for diamond to be converged. nshiftk 1 shiftk 0.0 0.0 0.0 # Ground state density iscf1 7 tolvrs1 1.0d-8 # tolvrs 1.0d-18 should be used for converged results # Non self-consistent calculation with an abritrary q point (here Gamma) getden2 1 iscf2 -2 nqpt2 1 qpt2 0.0 0.0 0.0 nbdbuf2 2 tolwfr2 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Computation at Gamma getwfk3 1 getwfq3 2 nqpt3 1 qpt3 0.0 0.0 0.0 # Calculation at Gamma ieig2rf3 1 # Static eigenvalues corrections using DFPT (Sternheimer) smdelta3 1 # Flag required to produce the _EIGI2D used to # compute the lifetime of electronic levels. # smdelta = 1 ==> Fermi-Dirac smearing. nbdbuf3 2 # 2 buffer bands. RF converges much faster. rfphon3 1 # Do phonon response rfatpol3 1 2 # Treat displacements of all atoms rfdir3 1 1 1 # Do all directions tolwfr3 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Cell dependant parameters acell 3*6.675 rprim 0 .5 .5 .5 0 .5 .5 .5 0 nsym 1 # Symmetries are not yet sufficiently tested. # Disable symmetries. natom 2 typat 1 1 xred 3*0.0 3*0.25 nband 12 ntypat 1 znucl 6 diemac 6 ecut 5 # Underconverged ecut. enunit 2 nstep 50 istwfk *1
You can use the following files file for abinit (will always be the same, just change the last digit for the other calculations):
- temp_1.files
temp_1.in temp_1.out temp_1i temp_1o temp_1 ../../../Psps_for_tests/6c.pspnc
If Abinit is compiled with Netcdf
If you have compiled Abinit with Netcdf, the calculation will produce _EIG.nc, _DDB, EIGR2D.nc and EIGI2D.nc that contain respectively the eigenvalues (GS or perturbed), the second-order derivative of the total energy with respect to two atomic displacement, the electron-phonon matrix elements used to compute the renormalization of the eigenenergies and the electron-phonon matrix elements used to compute the lifetime of the electronic states.
You can then copy the post-processing (PP-temperature) python file from ~/abinit/scripts/post_processing/temperature_para.py as well as the python file containing the required classes from ~/abinit/scripts/post_processing/mrgeignc.py into your current directory where you did the Abinit calculations.
You can then simply run the python script with the following command
python temperature_para.py
and enter the informations that the script ask.
For example a set of possible answer could be (please remove the comments if you plan to use this file as input for the script)
1 # Number of cpu to do the calculations
1 # Static ZPR computed in the Allen-Heine-Cardona (AHC) theory
temperature # Root name of the output
y # We want the ZPR AND the temperature dependence
1000 50 # We want the renormalization between 0 and 1000K by steps of 50K.
y
1 # Number of Q-points we have (here we only computed $\Gamma$)
temp_1o_DS3_DDB # Name of the response-funtion (RF) DDB file
temp_1o_DS2_EIG.nc # Eigenvalues at $\mathbf{k+q}$
temp_1o_DS3_EIGR2D.nc # Second-order electron-phonon matrix element
temp_1o_DS3_EIGI2D.nc # Second-order electron-phonon matrix element for electronic lifetime
temp_1o_DS1_EIG.nc # Eigenvalues at $k$
The python code will generate 3 files:
- temperature.txt: This text file contain the ZPM correction at each $\mathbf{k}$-points for each bands. It also contain the evolution of each band with temperature at $\mathbf{k}=\mathbf{\Gamma}$. At the end of the file, the Fan/DDW contribution is also reported.
- temperature_EP.nc This netcdf file contain a number for each $\mathbf{k}$-points, for each bands and each temperature. The real part of this number is the ZPM correction and the imaginary part is the lifetime
- temperature_BRD.txt This text file contain the lifetime of the electronic states at each $\mathbf{k}$-points for each bands. It also contain the evolution of each band with temperature at $\mathbf{k}=\mathbf{\Gamma}$.
We can for example visualize the temperature dependence at $\mathbf{k}=\Gamma$ of the HOMO bands with the contribution of only the $\mathbf{q}=\Gamma$ from the temperature.txt file.
The data plotter plugin is still experimental. Please check that everything is OK. Yann Pouillon, 2014/08/25
<dataplot smooth center xlabel=“Temperature (K)”> 0.0 -0.00632139604381 50.0 -0.00632139604381 100.0 -0.00632139605099 150.0 -0.00632140472083 200.0 -0.00632169751734 250.0 -0.0063239302778 300.0 -0.00633187859102 350.0 -0.00635032598464 400.0 -0.00638343533465 450.0 -0.00643390836627 500.0 -0.00650294484658 550.0 -0.00659057783023 600.0 -0.00669607434706 650.0 -0.00681826804029 700.0 -0.00695579453757 750.0 -0.00710724219667 800.0 -0.00727124090402 850.0 -0.00744650947655 900.0 -0.00763187703153 950.0 -0.00782628880673 </dataplot>
Here you can see that the HOMO correction goes down with temperature. This is due to the highly non-converged calculation. If you increase ecut from 5 to 10, you get the following plot.
<dataplot smooth center ylabel=r“$\Delta$E [eV]” xlabel=“Temperature (K)”> 0.0 0.0464879360158 50.0 0.0464879360158 100.0 0.046487936016 150.0 0.046487937587 200.0 0.0464880738214 250.0 0.0464899548307 300.0 0.0465000240982 350.0 0.0465313526812 400.0 0.0466012666529 450.0 0.0467271426935 500.0 0.0469232043665 550.0 0.0471991587068 600.0 0.0475602345155 650.0 0.0480079317466 700.0 0.0485409763626 750.0 0.0491562115748 800.0 0.049849321247 850.0 0.0506153700749 900.0 0.0514491834908 950.0 0.052345601391 </dataplot>
This means that the HOMO eigenenergies correction will go up with temperature. You can also plot the LUMO eigenenergies corrections and see that they go down. The ZPR correction as well as their temperature dependence usually closes the gap in semiconductors.
If Abinit is not compiled with Netcdf
Here we should first use mrgddb to merge the _DDB and _EIGR2D/_EIGI2D but since we only have one $\mathbf{q}$-point we do not have to do it.
The static temperature dependence as well as the G2F can be computed thanks to anaddb with the following files file:
- temp_2.files
temp_2.in temp_2.out temp_1o_DS3_DDB dummyo.md temp_1o_DS3_EIGR2D temp_2 dummy.ddk
and the following input file:
- temp_2.in
!Input file for the anaddb code. Analysis of the C DDB !Flags ifcflag 1 ! Interatomic force constant flag thmflag 3 telphint 1 ntemper 20 tempermin 1 temperinc 50 !Wavevector grid number 1 (coarse grid, from DDB) brav 1 ! Bravais Lattice : 1-S.C., 2-F.C., 3-B.C., 4-Hex.) ngqpt 1 1 1 ! Monkhorst-Pack indices nqshft 1 ! number of q-points in repeated basic q-cell q1shft 3*0.0 !Effective charges asr 1 ! Acoustic Sum Rule. 1 => imposed asymetrically chneut 1 ! Charge neutrality requirement for effective charges. !Interatomic force constant info dipdip 0 ! Dipole-dipole interaction treatment !Wavevector list number 1 (Reduced coordinates and normalization factor) nph1l 1 ! Number of phonons in list 1 qph1l 0.0 0.0 0.0 1.0
The run will create three files:
- temp_2.out_ep_G2F: This $g^2F$ spectral function represent the contribution of the phononic modes of energy E to the change of electronic eigenenergies according to the following equation
$g^2F(n\mathbf{k},E)=\sum_{\mathbf{q}m}\frac{\partial \varepsilon_{n\mathbf{k}}}{\partial n_m(\mathbf{q})}\delta(E-\hbar\omega_m(\mathbf{q}))$
- temp_2.out_ep_PDS: This file contains the phonon density of states
- temp_2.out_ep_TBS: This file contains the eigeneneriges corrections as well as the temperature dependence one. You can check that the results are the same as with the python script approach here above.
2. Converging the calculation with the $\mathbf{q}$-point grid
Starting now we are going to only describe the approach with Abinit compiled with Netcdf. The approach with Anaddb is similar to what we described above. Note that Anaddb only support homogenous $\mathbf{q}$-point integration.
You can integrate over the $\mathbf{q}$-grid using either random $\mathbf{q}$-point integration or homogenous Monkhorst-Pack based integration. For the random integration you should create a script that generate random $\mathbf{q}$-point, perform the Abinit calculations at these points and then integrate them using the temperature_para.py script. The script will detect that you did random integration thanks to the weight of the $\mathbf{q}$-point stored in the _EIGR2D.nc file and perform the integration accordingly. The random integration converges slowly but in a consistent manner. Since this methods is a little bit less user friendly we will focus on the homogenous integration.
The first thing we need to do is to determine the number of $\mathbf{q}$-point in the IBZ for a given $\mathbf{q}$-point grid. We choose here a 4x4x4 $\mathbf{q}$-point grid.
Using the following input file
- temp_3.in
# C in diamond structure. ndtset 3 udtset 1 3 iqpt:? 1 # Index of the first q-point of this file (usefull if you split your # input files elph2_imagden 0.1 eV # Imaginary shift of the denominator of the sum-over-states # in the perturbation denominator. Usual value is 0.1 eV to reproduce # experimental broadening at 300K. Increasing the value help the # convergence with respect to the number of q-points. ngkpt 2 2 2 # k-grid should be at least 4x4x4 for diamond to be converged. nshiftk 1 shiftk 0.0 0.0 0.0 ngqpt 4 4 4 # Should be converged upon qptopt 1 nshiftq 1 shiftq 0.0 0.0 0.0 # Ground state density iqpt+? 1 iscf?1 7 tolvrs?1 1.0d-8 # tolvrs 1.0d-18 should be used for converged results # Non self-consistent calculation with an abritrary q point (here Gamma) getden?2 -1 iscf?2 -2 nqpt?2 1 nbdbuf?2 2 tolwfr?2 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Computation at Gamma getwfk?3 -2 getwfq?3 -1 nqpt?3 1 ieig2rf?3 1 # Static eigenvalues corrections using DFPT (Sternheimer) smdelta?3 1 # Flag required to produce the _EIGI2D used to # compute the lifetime of electronic levels. # smdelta = 1 ==> Fermi-Dirac smearing. nbdbuf?3 2 # 2 buffer bands. RF converges much faster. rfphon?3 1 # Do phonon response rfatpol?3 1 2 # Treat displacements of all atoms rfdir?3 1 1 1 # Do all directions tolwfr?3 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Cell dependant parameters acell 3*6.675 rprim 0 .5 .5 .5 0 .5 .5 .5 0 nsym 1 # Symmetries are not yet sufficiently tested. # Disable symmetries. natom 2 typat 1 1 xred 3*0.0 3*0.25 nband 12 ntypat 1 znucl 6 diemac 6 ecut 5 # Underconverged ecut. enunit 2 nstep 50 istwfk *1
you can launch it and quickly kill the job. Then look into the log file to find the following line after the list of $\mathbf{q}$-points:
symkpt : the number of k-points, thanks to the symmetries, is reduced to 8
In general, in order to get the number of $\mathbf{q}$-points, you launch a “fake” run with a $\mathbf{k}$-point grid equivalent to the $\mathbf{q}$-point grid you want to use in your calculation.
Now that we know that the 4x4x4 $\mathbf{q}$-point grid reduces to 8 IBZ $\mathbf{q}$-point we can make the following substitution into the input file
ndtset 3 udtset 1 3 ==> ndtset 24 udtset 8 3
and then launch the calculation. When the Abinit run is finished you can launch the python script
python temperature_para.py < temperature3.files
with the following file
- temperature3.files
2 1 temperature3 y 1000 50 y 8 temp_3o_DS13_DDB temp_3o_DS23_DDB temp_3o_DS33_DDB temp_3o_DS43_DDB temp_3o_DS53_DDB temp_3o_DS63_DDB temp_3o_DS73_DDB temp_3o_DS83_DDB temp_3o_DS12_EIG.nc temp_3o_DS22_EIG.nc temp_3o_DS32_EIG.nc temp_3o_DS42_EIG.nc temp_3o_DS52_EIG.nc temp_3o_DS62_EIG.nc temp_3o_DS72_EIG.nc temp_3o_DS82_EIG.nc temp_3o_DS13_EIGR2D.nc temp_3o_DS23_EIGR2D.nc temp_3o_DS33_EIGR2D.nc temp_3o_DS43_EIGR2D.nc temp_3o_DS53_EIGR2D.nc temp_3o_DS63_EIGR2D.nc temp_3o_DS73_EIGR2D.nc temp_3o_DS83_EIGR2D.nc temp_3o_DS13_EIGI2D.nc temp_3o_DS23_EIGI2D.nc temp_3o_DS33_EIGI2D.nc temp_3o_DS43_EIGI2D.nc temp_3o_DS53_EIGI2D.nc temp_3o_DS63_EIGI2D.nc temp_3o_DS73_EIGI2D.nc temp_3o_DS83_EIGI2D.nc temp_3o_DS11_EIG.nc
The plotting of the same HOMO band at $\mathbf{k}=\mathbf{\Gamma}$ for a 4x4x4 $\mathbf{q}$-point grid gives a very different result than previously (this graph has been obtained with ecut = 10).
<dataplot smooth center xlabel=“Temperature (K)”> 0.0 0.166905716001 50.0 0.168134530003 100.0 0.175643958016 150.0 0.186487215252 200.0 0.19873983889 250.0 0.211833309088 300.0 0.225591061728 350.0 0.239951994749 400.0 0.25488503858 450.0 0.270361167392 500.0 0.286346138829 550.0 0.302800818967 600.0 0.319683636241 650.0 0.33695301779 700.0 0.354569157565 750.0 0.372495074865 800.0 0.390697117361 850.0 0.409145087192 900.0 0.427812136529 950.0 0.446674536837 </dataplot>
As a matter of fact, diamond needs an extremely dense $\mathbf{q}$-point grid (40x40x40) to be converged. On the bright side each $\mathbf{q}$-point calculation is independent and thus scales ideally…
3. Calculation of the eigenenergies correction along high-symmetry lines
The calculation of the electronic eigenvalue correction due to electron-phonon coupling along high-symmetry lines (also known as electronic bandstructure) require the use of 6 datasets per $\mathbf{q}$-points. Different datasets are required to compute the following quantites:
- 1. $\Psi_{\mathbf{k}_{HS}}^{(0)}$ the ground-state wavefunction on the Homogeneous $\mathbf{k}$-point sampling.
- 2. $\Psi_{\mathbf{k}_{BS}}^{(0)}$ the ground-state wavefunction computed along the bandstructure $\mathbf{k}$-point sampling.
- 3. $\Psi_{\mathbf{k}_{HS}+\mathbf{q}}^{(0)}$ the ground-state wavefunction on the shifted Homogeneous $\mathbf{k+q}$-point sampling.
- 4. $n^{(1)}$ The perturbed density integrated over the HS+q grid.
- 5. $\Psi_{\mathbf{k}_{BS}+\mathbf{q}}^{(0)}$ the ground-state wavefunction obtained from reading the perturbed density of the previous dataset
- 6. Reading the previous quantity we obtain the el-ph matrix elements along the BS with all physical quantities integrated over a HS grid.
- temp_4.in
# C in diamond structure. ndtset 48 udtset 8 6 iqpt:? 1 # Index of the first q-point of this file (usefull if you split your # input files elph2_imagden 0.1 eV # Imaginary shift of the denominator of the sum-over-states # in the perturbation denominator. Usual value is 0.1 eV to reproduce # experimental broadening at 300K. Increasing the value help the # convergence with respect to the number of q-points. ngkpt 2 2 2 # k-grid should be at least 4x4x4 for diamond to be converged. nshiftk 1 shiftk 0.0 0.0 0.0 ngqpt 4 4 4 # Should be converged upon qptopt 1 nshiftq 1 shiftq 0.0 0.0 0.0 # Ground state density iqpt+? 1 iscf?1 7 tolvrs?1 1.0d-8 # tolvrs 1.0d-18 should be used for converged results # Non self-consistent calculation following high sym k path getden?2 -1 iscf?2 -2 getwfk?2 -1 tolwfr?2 1.0d-8 # tolwfr 1.0d-22 should be used for converged results kptopt?2 -9 ndivsm?2 5 kptbounds?2 1/2 0.0 0.0 # L 0.0 0.0 0.0 # Gamma 0.0 1/2 1/2 # X 1/4 1/2 3/4 # W 3/8 3/8 3/4 # K 1/2 1/2 1/2 # L 1/4 1/2 3/4 # W 1/2 1/2 1.0 # X 3/8 3/8 3/4 # K 0.0 0.0 0.0 # Gamma # Non self-consistent calculation with an abritrary q point getden?3 -2 getwfk?3 -2 iscf?3 -2 nqpt?3 1 nbdbuf?3 2 tolwfr?3 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Computation at q getwfk?4 -3 getwfq?4 -1 iscf?4 7 nqpt?4 1 ieig2rf?4 1 # Static eigenvalues corrections using DFPT (Sternheimer) smdelta?4 1 # Flag required to produce the _EIGI2D used to # compute the lifetime of electronic levels. # smdelta = 1 ==> Fermi-Dirac smearing. nbdbuf?4 2 # 2 buffer bands. RF converges much faster. rfphon?4 1 # Do phonon response rfatpol?4 1 2 # Treat displacements of all atoms rfdir?4 1 1 1 # Do all directions tolwfr?4 1.0d-8 # tolwfr 1.0d-22 should be used for converged results # Non self-consistent calculation following high sym k path nqpt?5 1 getden?5 -4 iscf?5 -2 getwfk?5 -3 nbdbuf?5 2 # 2 buffer bands. RF converges much faster. tolwfr?5 1.0d-8 # tolwfr 1.0d-22 should be used for converged results kptopt?5 -9 ndivsm?5 5 kptbounds?5 1/2 0.0 0.0 # L 0.0 0.0 0.0 # Gamma 0.0 1/2 1/2 # X 1/4 1/2 3/4 # W 3/8 3/8 3/4 # K 1/2 1/2 1/2 # L 1/4 1/2 3/4 # W 1/2 1/2 1.0 # X 3/8 3/8 3/4 # K 0.0 0.0 0.0 # Gamma # Computation at an other q point nqpt?6 1 getden?6 -5 get1den?6 -2 getwfk?6 -4 getwfq?6 -1 tolwfr?6 1.0d-8 # tolwfr 1.0d-22 should be used for converged results nbdbuf?6 2 # 2 buffer bands. RF converges much faster. ieig2rf?6 1 smdelta?6 1 rfphon?6 1 rfatpol?6 1 2 rfdir?6 1 1 1 iscf?6 -2 kptopt?6 -9 ndivsm?6 5 kptbounds?6 1/2 0.0 0.0 # L 0.0 0.0 0.0 # Gamma 0.0 1/2 1/2 # X 1/4 1/2 3/4 # W 3/8 3/8 3/4 # K 1/2 1/2 1/2 # L 1/4 1/2 3/4 # W 1/2 1/2 1.0 # X 3/8 3/8 3/4 # K 0.0 0.0 0.0 # Gamma # Cell dependant parameters acell 3*6.675 rprim 0 .5 .5 .5 0 .5 .5 .5 0 nsym 1 # Symmetries are not yet sufficiently tested. # Disable symmetries. natom 2 typat 1 1 xred 3*0.0 3*0.25 nband 12 ntypat 1 znucl 6 diemac 6 ecut 5 # Underconverged ecut. enunit 2 nstep 50 istwfk *1
Using the following files file for the python script
- temperature4.files
1 1 temperature4 y 1000 50 y 8 temp_4o_DS14_DDB temp_4o_DS24_DDB temp_4o_DS34_DDB temp_4o_DS44_DDB temp_4o_DS54_DDB temp_4o_DS64_DDB temp_4o_DS74_DDB temp_4o_DS84_DDB temp_4o_DS15_EIG.nc temp_4o_DS25_EIG.nc temp_4o_DS35_EIG.nc temp_4o_DS45_EIG.nc temp_4o_DS55_EIG.nc temp_4o_DS65_EIG.nc temp_4o_DS75_EIG.nc temp_4o_DS85_EIG.nc temp_4o_DS16_EIGR2D.nc temp_4o_DS26_EIGR2D.nc temp_4o_DS36_EIGR2D.nc temp_4o_DS46_EIGR2D.nc temp_4o_DS56_EIGR2D.nc temp_4o_DS66_EIGR2D.nc temp_4o_DS76_EIGR2D.nc temp_4o_DS86_EIGR2D.nc temp_4o_DS16_EIGI2D.nc temp_4o_DS26_EIGI2D.nc temp_4o_DS36_EIGI2D.nc temp_4o_DS46_EIGI2D.nc temp_4o_DS56_EIGI2D.nc temp_4o_DS66_EIGI2D.nc temp_4o_DS76_EIGI2D.nc temp_4o_DS86_EIGI2D.nc temp_4o_DS12_EIG.nc
Off course the high symmetry points that we computed in section 2 have the same value here. It is a good idea to check it by running the following script file
- temperature3_bis.files
1 1 temperature4_bis y 1000 50 y 8 temp_4o_DS14_DDB temp_4o_DS24_DDB temp_4o_DS34_DDB temp_4o_DS44_DDB temp_4o_DS54_DDB temp_4o_DS64_DDB temp_4o_DS74_DDB temp_4o_DS84_DDB temp_4o_DS13_EIG.nc temp_4o_DS23_EIG.nc temp_4o_DS33_EIG.nc temp_4o_DS43_EIG.nc temp_4o_DS53_EIG.nc temp_4o_DS63_EIG.nc temp_4o_DS73_EIG.nc temp_4o_DS83_EIG.nc temp_4o_DS14_EIGR2D.nc temp_4o_DS24_EIGR2D.nc temp_4o_DS34_EIGR2D.nc temp_4o_DS44_EIGR2D.nc temp_4o_DS54_EIGR2D.nc temp_4o_DS64_EIGR2D.nc temp_4o_DS74_EIGR2D.nc temp_4o_DS84_EIGR2D.nc temp_4o_DS14_EIGI2D.nc temp_4o_DS24_EIGI2D.nc temp_4o_DS34_EIGI2D.nc temp_4o_DS44_EIGI2D.nc temp_4o_DS54_EIGI2D.nc temp_4o_DS64_EIGI2D.nc temp_4o_DS74_EIGI2D.nc temp_4o_DS84_EIGI2D.nc temp_4o_DS11_EIG.nc
You can then copy the plotting script (Plot-EP-BS) python file from ~/abinit/scripts/post_processing/plot_bs.py into your current directory where you did the Abinit calculations. Note that in order to run this script you need the following requirement
- python 2.7.6 or higher
- numpy 1.7.1 or higher
- netCDF4 and netCDF4 for python
- scipy 0.12.0 or higher
You can then use the following script feeding file or enter the data manually
- plot_bs.files
temperature4_EP.nc L \Gamma X W K L W X K \Gamma -20 30 0
This should give you the following bandstructure:
where the solid black lines are the traditional electronic bandstructure, the dased lines are the electronic eigenenergies with electron-phonon renormalization at a defined temperature (here 0K). Finally the area around the dashed line is the lifetime of the electronic eigenstates.
You should of course notice all the spiky jumps in the renormalization. This is due to the fact that we did a completely under-converged calculation.
It is possible to converge the calculations using an ecut of 30 Ha, a ngkpt grid of 6x6x6 and an increasing ngqpt grid to get converged results:
| Convergence study ZPR and lifetime [meV] at 0K | |||||||
|---|---|---|---|---|---|---|---|
| q-grid | Nb qpt in IBZ | $k=\Gamma_{25'}$ | Broadening | $k=\Gamma_{15}$ | Lifetime | $k=(\Gamma-X)$ | Broadening |
| 4x4x4 | 8 | 0.1175 | 0.0701 | -0.3178 | 0.1916 | -0.1570 | 0.0250 |
| 10x10x10 | 47 | 0.1390 | 0.0580 | -0.3288 | 0.1847 | -0.1605 | 0.0308 |
| 20x20x20 | 256 | 0.1446 | 0.0574 | -0.2691 | 0.1823 | -0.1592 | 0.0298 |
| 26x26x26 | 511 | 0.1448 | 0.0573 | -0.2736 | 0.1823 | -0.1592 | 0.0297 |
| 34x34x34 | 1059 | 0.1446 | 0.0573 | -0.2699 | 0.1821 | -0.1591 | 0.0297 |
| 43x43x43 | 2024 | 0.1447 | 0.0572 | -0.2650 | 0.1821 | -0.1592 | 0.0297 |
As you can see the limiting factor for the convergence study is the convergence of the LUMO band at $k=\Gamma$. This band is not the lowest in energy (the lowest in on the line between $\Gamma$ and $X$) and therefore this band is rather unstable. This can also be seen by the fact that it has a large electronic broadening, meaning that this state will decay quickly into another state.
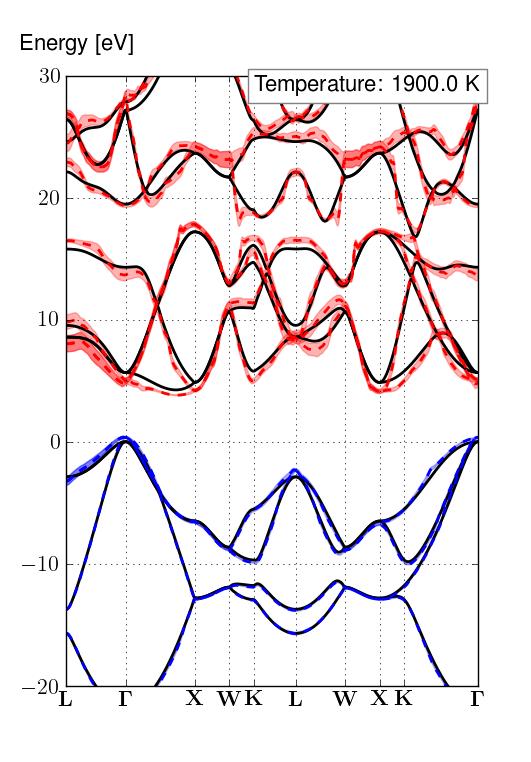
Using the relatively dense $\mathbf{q}$-grid of 43x43x43 we can obtain the following converged bandstructure:
Here we show the renormalization at a very high temperature of 1900K in order to highlight more the broadening and renormalization that occurs. If you want accurate values of the ZPR at 0K you can look at the table above.
Possible issue while converging your calculations
If you use a extremely fine $\mathbf{q}$-point grid, the acoustic phonon frequencies for $\mathbf{q}$-points close to $\Gamma$ will be wrongly determined by Abinit. Indeed in order to have correct phonon frequencies, you have to impose the accousting sum rule with anaddb. Since it is not possible here with the script, we reject the contribution of the acoustic phonon close to $\Gamma$ if their phonon frequency is lower than 1E-6 Ha. Otherwise you get unphysically large contribution. You can tune this paramter by editing the variable “tol6 = 1E-6” in the beginning of the mrgeignc.py file. For example, for the last 43x43x43 calculation, I had to set it to 1E-4.